Лабораторная работа №1
Тема: «Приближенное решение уравнений»
Отчет
1.Постановка задачи
Вычислить уравнение: x*ln(x)=100 с точностью до Ɛ=〖10〗^(-5)
2.Выделим интервал, на котором существует единственный корень
X=1 => y= -100;
X=50 => y=95.6;
Так как значение функции меняет свой знак на интервале (1;50), то на этом интервале существует по крайней мере 1 корень (по теореме 1). Корень будет единственным, если первая производная функции на этом интервале не меняет своего значения:
〖y^ʹ=ln〗(x)+1>0 на интервале (1;50) , следовательно, на данном интервале корень 1.
Воспользуемся методом итерации, для выбора формулы необходимо найти 2 производную y^(ʹʹ)=1/(x )> 0 на интервале (1;50).
3.Вычисление корня уравнения
Метод итерации
Для применения этого метода исходное уравнение должно быть приведено эквивалентными преобразованиями к виду .
Выбрав начальное приближение и подставив его в правую часть уравнения , получим . Повторяя этот процесс, получаем числовую последовательность . Для сходимости процесса необходимо обеспечить выполнение условия и чем ближе значение к 0, тем быстрее сходится процесс.
Для приведения исходного уравнения к виду умножим обе его части на –λ
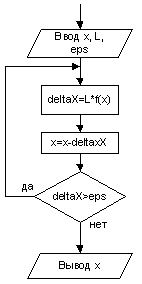
Прибавим слева и справа x
Обозначим , и найдём производную . На интервале [a, b] . Можем выбрать значение , а знак λ совпадал бы со знаком на [a, b].
Условие окончания процесса уточнения корня
Итерационный процесс сходится к корню уравнения 29,5365. Процесс завершился после 8-ти итераций.
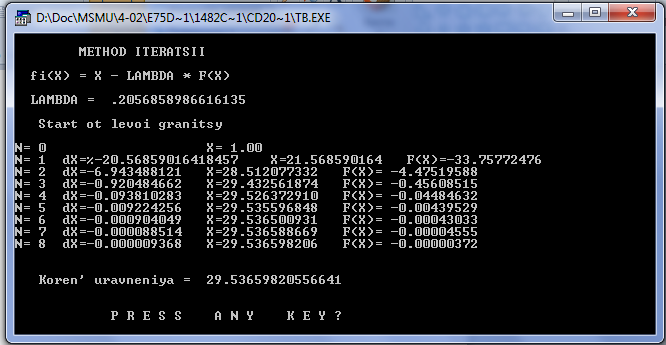
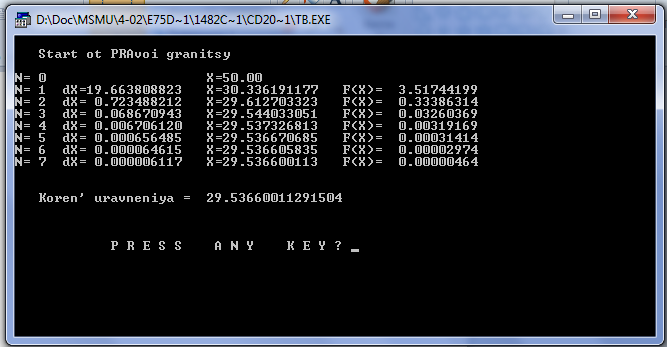
Метод хорд
В основе метода лежит линейная интерполяция функции по двум значениям, имеющим противоположные знаки. Очередное приближение берём в точке пересечения с осью ОХ прямой, соединяющей точки (a, f(a)) и (b, f(b)). Формулу для уточнения корня выбираем по следующему условию
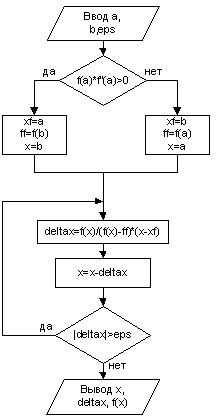
если , то (3)
если , то (4)
На самом первом шаге вычислений принимаем нулевое приближение корня
в случае (3) , в случае (4) .
Условие окончания процесса уточнения корня
в первом случае (5)
во втором случае . (6)
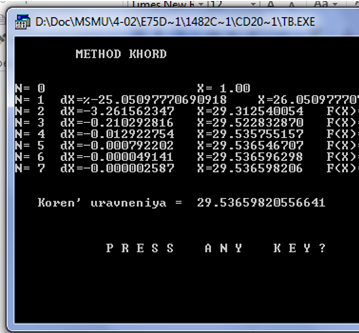
Метод Ньютона
Метод основан на замене f(x) в точке начального приближения x0 касательной, пересечение которой с осью OX даёт первое приближение x1, и т.д. Вместо интерполяции по двум значениям метод Ньютона использует экстраполяцию с помощью касательной в данной точке. Процесс сходится, если в области поиска корня производная f'(x) ≠ 0 и f(x)•f''(x) > 0. В качестве нулевого приближения выбираем тот конец отрезка, где выполняется условие f(x)•f''(x) > 0. В общем случае очередное приближение xn+1 выражается через предыдущее приближение xn по формуле
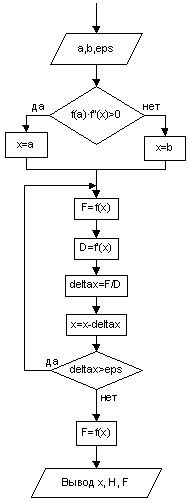
, (7)
Условие окончания процесса уточнения корня
(8)
Общая расчётная формула
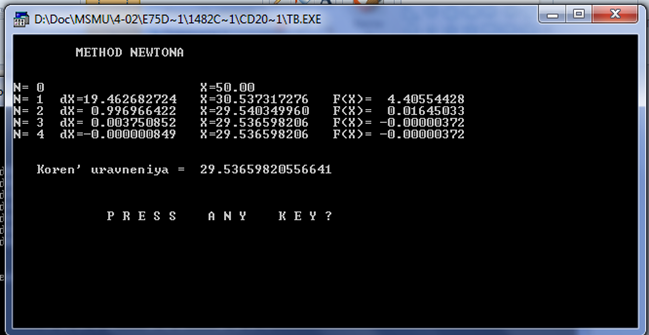
Метод Рыбакова
Этот метод является модификацией метода Ньютона. Алгоритм осуществляет поиск всех корней на заданном промежутке [a, b]. Чтобы условия сходимости были выполнены на всём интервале, производная заменена некоторой константой M, которая выбирается из условия
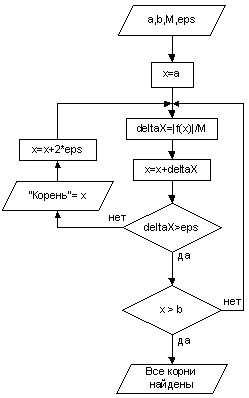
Условие окончания процесса уточнения корня
(10)
Для перехода к поиску и уточнению следующего корня, уже найденное значение увеличим на 2ε и запустим процесс уточнения корня. И так до тех пор, пока .
В качестве М возьмем 60.
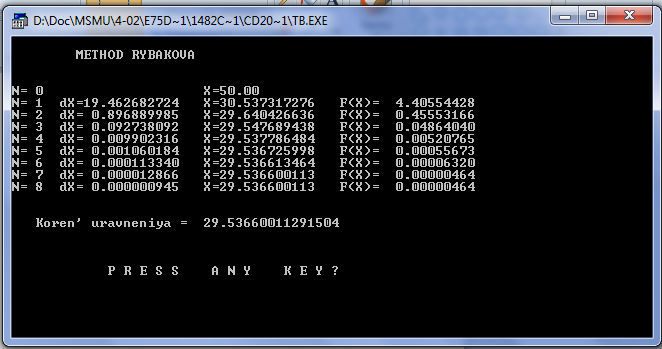
Выполним вычисление корня уравнения в одной программе, ниже приведен код программы
DEF FNF(X) = log(X)*X-100
DEF FNF1(X) = log(X)+1
DEF FNF2(X) = 1/X
10 CLS
INPUT " Input start point ";XL
INPUT " Input end point ";XR
LOCATE 4,1: PRINT "X"
LOCATE 5,1: PRINT "F"
LOCATE 6,1: PRINT "F'"
LOCATE 7,1: PRINT "F''"
P=5
FOR X=XL TO XR STEP (XR-XL)/10
LOCATE 4,P: PRINT USING "###.##";X
LOCATE 5,P: PRINT USING "###.##";FNF(X)
LOCATE 6,P: PRINT USING "###.##";FNF1(X)
LOCATE 7,P: PRINT USING "###.##";FNF2(X)
P=P+7
NEXT
PRINT: PRINT
INPUT " It's OK? (1 - YES, 0 - NO) ";ANS
IF ANS<>1 THEN GOTO 10
PRINT: PRINT
INPUT " Input LEFT point ";A
INPUT " Input RIGHT point ";B
PRINT
INPUT " Tochnost' = ";EPS
FRMT$="###."
E1=EPS
WHILE CINT(E1)0 THEN
Xfix=A
Ffix=FNF(A)
X=B
ELSE
Xfix=B
Ffix=FNF(B)
X=A
END IF
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX/(FX-Ffix)*(X-Xfix)
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
KHORDY=X
N1=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT
PRINT " METHOD NEWTONA"
PRINT
IF FNF(A)*FNF2(A)>0 THEN X=A ELSE X=B
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX/FNF1(X)
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
NEWTON=X
N2=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT
PRINT " METHOD RYBAKOVA"
PRINT
IF FNF(A)*FNF2(A)>0 THEN X=A ELSE X=B
M=FNF1(X)
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX/M
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
RYBAKOV=X
N3=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT
PRINT " METHOD ITERATSII"
PRINT
PRINT " fi(X) = X - LAMBDA * F(X)"
PRINT
REM PRINT " PODBOR LAMBDA"
MAX=FNF1(A)
FOR X=A TO B STEP (B-A)/20
rem FS=ABS(FNF1(X))
IF ABS(FNF1(X))>ABS(MAX) THEN MAX=FNF1(X)
NEXT X
LAMBDA=1/MAX
PRINT " LAMBDA = ";LAMBDA
PRINT
PRINT " Start ot levoi granitsy"
X=A
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX*LAMBDA
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
ITERLeft=X
N4=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT
PRINT " Start ot PRAvoi granitsy"
X=B
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX*LAMBDA
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
ITERRight=X
N5=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT: PRINT: PRINT
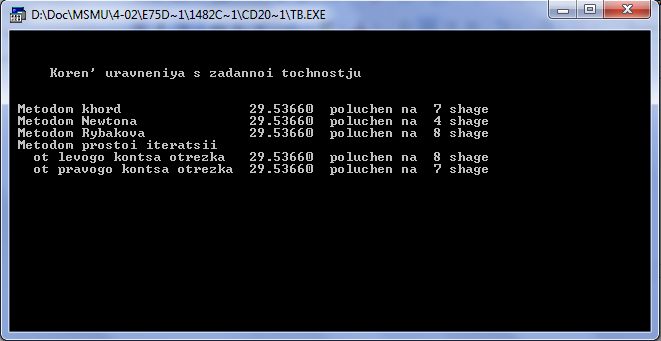
PRINT " Koren' uravneniya s zadannoi tochnostju "
PRINT: PRINT
PRINT USING " Metodom khord "+FRMT$+" poluchen na ## shage";KHORDY,N1
PRINT USING " Metodom Newtona "+FRMT$+" poluchen na ## shage";NEWTON,N2
PRINT USING " Metodom Rybakova "+FRMT$+" poluchen na ## shage";RYBAKOV,N3
PRINT " Metodom prostoi iteratsii"
PRINT USING " ot levogo kontsa otrezka "+FRMT$+" poluchen na ## shage";ITERLeft,N4
PRINT USING " ot pravogo kontsa otrezka "+FRMT$+" poluchen na ## shage";ITERRight,N5
STOP
SHOW:
PRINT USING "N=## dX=##.######### X=##.######### F(X)=###.########";N,DeltaX,X,FX
RETURN
4. Итоги и выводы
Все рассмотренные методы решения неоднородных уравнений есть некоторый сходящийся итерационный процесс, выражаемый общим уравнением
, (мы эту величину обозначали ),
пределом которого является корень уравнения
Слагаемое h имеет вид , где параметр T для каждого метода имеет определённое значение.
В методе хорд
(С1 и с2 – это некоторые постоянные)
и в методе Ньютона
это переменная величина, вычисляемая на каждой итерации.
А в методе Рыбакова
, ,
и в методе простой итерации
, на
Тема: «Приближенное решение уравнений»
Отчет
1.Постановка задачи
Вычислить уравнение: x*ln(x)=100 с точностью до Ɛ=〖10〗^(-5)
2.Выделим интервал, на котором существует единственный корень
X=1 => y= -100;
X=50 => y=95.6;
Так как значение функции меняет свой знак на интервале (1;50), то на этом интервале существует по крайней мере 1 корень (по теореме 1). Корень будет единственным, если первая производная функции на этом интервале не меняет своего значения:
〖y^ʹ=ln〗(x)+1>0 на интервале (1;50) , следовательно, на данном интервале корень 1.
Воспользуемся методом итерации, для выбора формулы необходимо найти 2 производную y^(ʹʹ)=1/(x )> 0 на интервале (1;50).
3.Вычисление корня уравнения
Метод итерации
Для применения этого метода исходное уравнение должно быть приведено эквивалентными преобразованиями к виду .
Выбрав начальное приближение и подставив его в правую часть уравнения , получим . Повторяя этот процесс, получаем числовую последовательность . Для сходимости процесса необходимо обеспечить выполнение условия и чем ближе значение к 0, тем быстрее сходится процесс.
Для приведения исходного уравнения к виду умножим обе его части на –λ

Прибавим слева и справа x
Обозначим , и найдём производную . На интервале [a, b] . Можем выбрать значение , а знак λ совпадал бы со знаком на [a, b].
Условие окончания процесса уточнения корня
Итерационный процесс сходится к корню уравнения 29,5365. Процесс завершился после 8-ти итераций.


Метод хорд
В основе метода лежит линейная интерполяция функции по двум значениям, имеющим противоположные знаки. Очередное приближение берём в точке пересечения с осью ОХ прямой, соединяющей точки (a, f(a)) и (b, f(b)). Формулу для уточнения корня выбираем по следующему условию

если , то (3)
если , то (4)
На самом первом шаге вычислений принимаем нулевое приближение корня
в случае (3) , в случае (4) .
Условие окончания процесса уточнения корня
в первом случае (5)
во втором случае . (6)

Метод Ньютона
Метод основан на замене f(x) в точке начального приближения x0 касательной, пересечение которой с осью OX даёт первое приближение x1, и т.д. Вместо интерполяции по двум значениям метод Ньютона использует экстраполяцию с помощью касательной в данной точке. Процесс сходится, если в области поиска корня производная f'(x) ≠ 0 и f(x)•f''(x) > 0. В качестве нулевого приближения выбираем тот конец отрезка, где выполняется условие f(x)•f''(x) > 0. В общем случае очередное приближение xn+1 выражается через предыдущее приближение xn по формуле

, (7)
Условие окончания процесса уточнения корня
(8)
Общая расчётная формула

Метод Рыбакова
Этот метод является модификацией метода Ньютона. Алгоритм осуществляет поиск всех корней на заданном промежутке [a, b]. Чтобы условия сходимости были выполнены на всём интервале, производная заменена некоторой константой M, которая выбирается из условия

Условие окончания процесса уточнения корня
(10)
Для перехода к поиску и уточнению следующего корня, уже найденное значение увеличим на 2ε и запустим процесс уточнения корня. И так до тех пор, пока .
В качестве М возьмем 60.

Выполним вычисление корня уравнения в одной программе, ниже приведен код программы
DEF FNF(X) = log(X)*X-100
DEF FNF1(X) = log(X)+1
DEF FNF2(X) = 1/X
10 CLS
INPUT " Input start point ";XL
INPUT " Input end point ";XR
LOCATE 4,1: PRINT "X"
LOCATE 5,1: PRINT "F"
LOCATE 6,1: PRINT "F'"
LOCATE 7,1: PRINT "F''"
P=5
FOR X=XL TO XR STEP (XR-XL)/10
LOCATE 4,P: PRINT USING "###.##";X
LOCATE 5,P: PRINT USING "###.##";FNF(X)
LOCATE 6,P: PRINT USING "###.##";FNF1(X)
LOCATE 7,P: PRINT USING "###.##";FNF2(X)
P=P+7
NEXT
PRINT: PRINT
INPUT " It's OK? (1 - YES, 0 - NO) ";ANS
IF ANS<>1 THEN GOTO 10
PRINT: PRINT
INPUT " Input LEFT point ";A
INPUT " Input RIGHT point ";B
INPUT " Tochnost' = ";EPS
FRMT$="###."
E1=EPS
WHILE CINT(E1)0 THEN
Xfix=A
Ffix=FNF(A)
X=B
ELSE
Xfix=B
Ffix=FNF(B)
X=A
END IF
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX/(FX-Ffix)*(X-Xfix)
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
KHORDY=X
N1=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT " METHOD NEWTONA"
IF FNF(A)*FNF2(A)>0 THEN X=A ELSE X=B
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX/FNF1(X)
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
NEWTON=X
N2=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT " METHOD RYBAKOVA"
IF FNF(A)*FNF2(A)>0 THEN X=A ELSE X=B
M=FNF1(X)
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX/M
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
RYBAKOV=X
N3=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT " METHOD ITERATSII"
PRINT " fi(X) = X - LAMBDA * F(X)"
REM PRINT " PODBOR LAMBDA"
MAX=FNF1(A)
FOR X=A TO B STEP (B-A)/20
rem FS=ABS(FNF1(X))
IF ABS(FNF1(X))>ABS(MAX) THEN MAX=FNF1(X)
NEXT X
LAMBDA=1/MAX
PRINT " LAMBDA = ";LAMBDA
PRINT " Start ot levoi granitsy"
X=A
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX*LAMBDA
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
ITERLeft=X
N4=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT " Start ot PRAvoi granitsy"
X=B
N=0
PRINT: PRINT USING "N=## X=##.##";N,X
FX=FNF(X)
DO
N=N+1
DeltaX=FX*LAMBDA
X=X-DeltaX
FX=FNF(X)
GOSUB SHOW
LOOP WHILE ABS(DeltaX)>EPS
ITERRight=X
N5=N
PRINT: PRINT
PRINT " Koren' uravneniya = ";X
PRINT: PRINT: PRINT
INPUT " P R E S S A N Y K E Y ";T
CLS
PRINT: PRINT: PRINT
PRINT " Koren' uravneniya s zadannoi tochnostju "
PRINT: PRINT
PRINT USING " Metodom khord "+FRMT$+" poluchen na ## shage";KHORDY,N1
PRINT USING " Metodom Newtona "+FRMT$+" poluchen na ## shage";NEWTON,N2
PRINT USING " Metodom Rybakova "+FRMT$+" poluchen na ## shage";RYBAKOV,N3
PRINT " Metodom prostoi iteratsii"
PRINT USING " ot levogo kontsa otrezka "+FRMT$+" poluchen na ## shage";ITERLeft,N4
PRINT USING " ot pravogo kontsa otrezka "+FRMT$+" poluchen na ## shage";ITERRight,N5
STOP
SHOW:
PRINT USING "N=## dX=##.######### X=##.######### F(X)=###.########";N,DeltaX,X,FX
RETURN
4. Итоги и выводы

Все рассмотренные методы решения неоднородных уравнений есть некоторый сходящийся итерационный процесс, выражаемый общим уравнением
, (мы эту величину обозначали ),
пределом которого является корень уравнения
Слагаемое h имеет вид , где параметр T для каждого метода имеет определённое значение.
В методе хорд
(С1 и с2 – это некоторые постоянные)
и в методе Ньютона
это переменная величина, вычисляемая на каждой итерации.
А в методе Рыбакова
, ,
и в методе простой итерации
, на