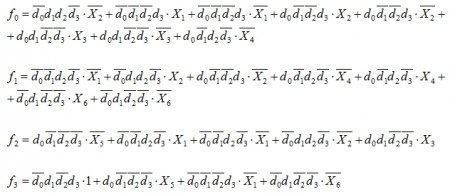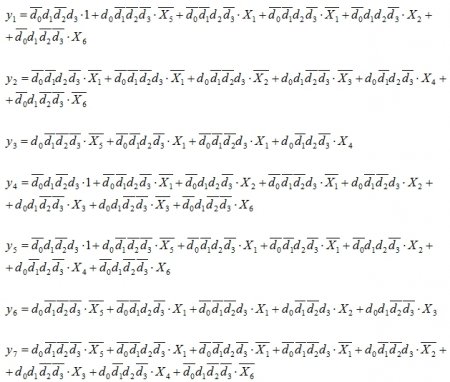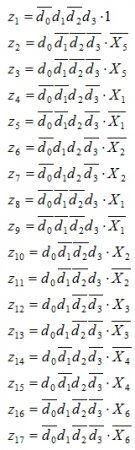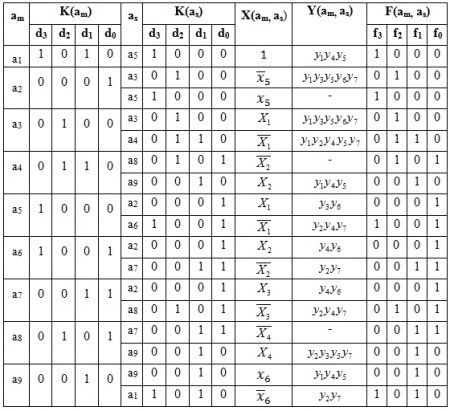
Расширенная структурная таблица переходов и выходов строится на основе прямой таблицы переходов и выходов (таблица 2.1) и результатов кодирования внутренних состояний синхронного УА (таблица 2.3). Для синхронного УА типа Мили результат представлен в таблице 3.1.



Таблица 3.1 - Расширенная структурная таблица переходов и выходов



В таблице 3.1 приняты следующие обозначения: am – состояние, в котором находится УА в текущий момент времени, К(am) – структурный код am, as – следующее состояние автомата, К(as) – структурный код as, X (am, as) – условие перехода из состояния am в состояние as, Y (am, as) – микрокоманда, выполняемая автоматом из am в as, F(am, as) – функция возбуждения элементов памяти.

3.2 Составление логических уравнений для выходных сигналов и функций возбуждения триггеров

Составление логических уравнений для функций возбуждения блока памяти F(аm, аs) сводится к составлению совокупности логических уравнений для каждой отдельной функции возбуждения элементов памяти f1…fr. Логические уравнения f1…fr записываются как дизъюнкция конъюнкций структурного кода исходного состояния автомата K(am) и комбинации входных сигналов X(аm, аs) по тем строкам таблицы 3.1, в которых в соответствующем столбце fi присутствует значение, равное 1.
Таким образом, получаем:



Функции выходов yi для автомата типа Мили представляют собой дизъюнкции конъюнкций структурного кода исходного состояния автомата K(am) по тем строкам структурной таблицы 3.1, в которых присутствует выходной сигнал yi, домноженного на условие перехода в новое состояние.
Таким образом, имеем:



Совокупность функций возбуждения элементов памяти f0…f3 и функций выходов y1…y7 представляют собой систему логических уравнений, которую необходимо минимизировать с целью упрощения схемы электрической функциональной УА.

3.3 Минимизация логических уравнений

Как было отмечено ранее, для реализации синхронного УА с применением ПЛМ целесообразно использовать метод групповой минимизации, поскольку классические методы, например, Квайна или карт Карно, в данном случае недостаточно эффективны.

Для групповой минимизации системы логических уравнений необходимо для одинаковых элементарных конъюнкций ввести фиктивные переменные следующим образом.



В результате замены фиктивными переменными конъюнкций функций возбуждения элементов памяти f0…f3 и функций выходов y1…y7 получим следующие минимизированные логические уравнения:




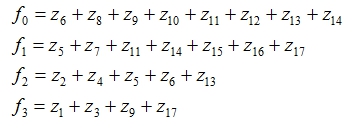
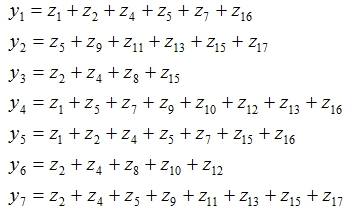
Набор полученных выражений представляет собой систему минимизированных логических уравнений, являющуюся входными данными для дальнейшего синтеза схемы электрической функциональной.