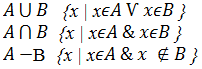Вопрос № 14 Реляционное исчисление - высокоуровневый непроцедурный язык .
Выражение реляционного исчисления описывает результирующее отношение, не регламентируя при этом способ получения этого результата. Термин «исчисление» заимствован из раздела математической логики – теория предикатов. Предикат P(x) логическая или истинностная функция. Множество значений x для которых используется P(x) {x| P(x) } В реляционных исчислениях в качестве переменной x могут выступать картежи или домены, т.о. реляционные исчисления делятся на: исчисляемые картежи, исчисляемые домены. Мы коснемся только исчисляемых картежей. В этом случае в выражение реляционного исчисления описывается множество картежей для которых истины предикаты(высказывание). При этом задается так же область определенных картежей, т.е. принадлежность картежей тому или иному отношению. Общая схема реляционного исчисления range x is R а также {x| P(x) }, x – результат выполнения запроса; P(x) – запрос.
Пример.
Выбрать коды аб, которые набрали в процесе тестирования больше 60 баллов
range x is B
{x.код аб | x.кол-во баллов>60 }
В выражениях реляционного исчисления используются кванторы существования и общности. Квантер существования ( ) обозначается, что в отношение существуют картежи для которых предикат истинен. Квантор общности ( ) обозначает, что квантор истинен для каждого картежа.
Пример.
Вывести фамилии аб набравших больше 60 баллов по результатам тестирования.
range x is B
range y is A
{x.фио | y(y.код = y.код аб & y.кол.б.>60 }
Реляционная алгебра и реляционное исчисление эквивалентны. Это обозначает, что каждому оператору реляционной алгебры можно привести в соответсвии выражение реляционного исчисления и наоборот.
Пример
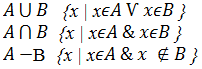
Выражение реляционного исчисления описывает результирующее отношение, не регламентируя при этом способ получения этого результата. Термин «исчисление» заимствован из раздела математической логики – теория предикатов. Предикат P(x) логическая или истинностная функция. Множество значений x для которых используется P(x) {x| P(x) } В реляционных исчислениях в качестве переменной x могут выступать картежи или домены, т.о. реляционные исчисления делятся на: исчисляемые картежи, исчисляемые домены. Мы коснемся только исчисляемых картежей. В этом случае в выражение реляционного исчисления описывается множество картежей для которых истины предикаты(высказывание). При этом задается так же область определенных картежей, т.е. принадлежность картежей тому или иному отношению. Общая схема реляционного исчисления range x is R а также {x| P(x) }, x – результат выполнения запроса; P(x) – запрос.
Пример.
Выбрать коды аб, которые набрали в процесе тестирования больше 60 баллов
range x is B
{x.код аб | x.кол-во баллов>60 }
В выражениях реляционного исчисления используются кванторы существования и общности. Квантер существования ( ) обозначается, что в отношение существуют картежи для которых предикат истинен. Квантор общности ( ) обозначает, что квантор истинен для каждого картежа.
Пример.
Вывести фамилии аб набравших больше 60 баллов по результатам тестирования.
range x is B
range y is A
{x.фио | y(y.код = y.код аб & y.кол.б.>60 }
Реляционная алгебра и реляционное исчисление эквивалентны. Это обозначает, что каждому оператору реляционной алгебры можно привести в соответсвии выражение реляционного исчисления и наоборот.
Пример